Liang Pei (裴亮)
Phys. H McLaughlin
Due Date: Tuesday, November 13, 2001

Laser Lab – Finding Young’s Modulus

             The purpose of the lab was to find the Young’s Modulus for a length of steel piano wire. The wire was set up in a device shown below. A collar was attached to the wire. The wire goes through an adjustable platform with a hole in it. The platform was adjusted so that when the wire was not under stress, the top of the collar would horizontally align with the top of the platform. To calculate Dl for Young’s Modulus, we could find the distance the collar moved below the top of the platform, when stress is applied to the wire. Since this distance was too small to measure, it must be found indirectly. We used an optical lever arm (a laser) to increase the scale of the distance so a more accurate measurement could be made. A mirror, with a perpendicular base was rested upon the platform and the collar by 3 pointed tips. Two tips rested in a groove on the platform while the 3^rd rested on a track on the collar. When the platform and the collar were on different levels (the wire under stress), the base, and thus the mirror, would be tipped. A laser was pointed at the mirror, so it would bounce off and the black board at the other end of the setup. Different amounts of stress were applied to the piano wire by hanging masses at the bottom. For each stress level, the point that was reflected onto the board was marked.

            We measured the following lengths:

            In order to calculate the Young’s Modulus, we must find each element of the formula: . We measured l (initial length of wire) directly. We measured the diameter of the wire with a micrometer so that we could find A (cross-sectional area) with the area of a circle formula: A=pr²; r=^d/_2; \A=p( ^d/₂)². We can calculate F (force applied to wire) easily by multiplying the mass we hooked on to the wire by gravitational acceleration (F=ma).

            To calculate Dl, we can use the relationships between triangles. Since at first, the collar and platform are on the same level, the mirror is perpendicular to both. The laser should reflect off the mirror and bounce directly back at the laser head. We had adjusted the overhead angle of the mirror so that the laser beam would go past the laser emitter itself and hit the black board instead. The distance between the board and the mirror is represented as D in the diagram below.

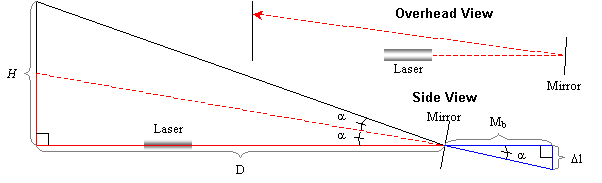
In the diagram, H is the distance between the first marked value on the board (initial stress=0) and another marked point that represents greater stress applied. Lets call this amount of stress ‘S’. When ‘S’ is applied to the wire, the collar moves downward. Thus, the collar and platform are at different levels. Since the base of the mirror rests on these 2 surfaces, the mirror tips slightly backwards. When the laser beam strikes the mirror, it now reflects and strikes the board at a higher level.

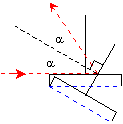According to the law of reflection, the incidence ray (from the source), reflection ray (after reflection), and normal of the mirror (line perpendicular to the mirror face) form 2 equal angles. The incidence ray and the normal form the incidence angle. The reflection ray and the normal form the reflection angle. One of these angles (alpha) is equal to the angle formed by the base of the tilted mirror and the initial base of the mirror.

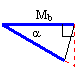
This triangle, represented in blue (thick lines) in the figure at right, is an isosceles triangle (the base remains the same length). We want the vertical distance between the far ends of the two bases. We can extend the figure into a right triangle for easier calculation. Although it is not totally accurate, the error is minimal since angle alpha is so small. This would give a slightly longer length than the actual length. However, since the mirror rests in grooves and the base length remains constant, the wire is pulled slightly towards the laser as the collar moves down. This would move the collar slightly upwards (compared to the actual Dl). The upward motion of the collar and the overestimation of Dl should result in an extremely small error.

The longer leg of this right triangle is the base of the mirror (M_b) and the shorter leg is the estimated Dl. The angle between the hypotenuse and the longer leg is alpha. We can find alpha from the right triangle formed by H, D and a third segment joining the two. Since we measured both H and D, we can find alpha: . After finding alpha, we can find Dl in the other triangle: .

Since our literature value is in N/m², we will be working in the mks system. The length of the wire is 0.637 m. The cross-sectional area of the wire is 2.565 x 10^-7 m². The force and Dl values are as follows:

The calculated Young’s Modulus values are as follows:

             The literature value for young’s modulus of steel (the piano wire is steel), according to problem set #19 is 1.92 x 10¹¹. We can calculate the percent error accuracy based on this value: . The results are as follows:

             It makes sense that as force increases the error decreases. This is because as force increases, alpha and Dl increase also. As Dl increases, the optical lever arm becomes more effective and accurate. However, we do not know whether 1.92E11 is really the literature value for the piano wire since there are many different types of steel. Proportionally, Dl is probably the most error-saturated value among the 4 variables of Young’s Modulus.

            The GPE of each measured value are as follows:

           Our equation for Young’s Modulus is: . We must find the percent error of each of the 4 variables and add them for the total percent error of Young’s Modulus. The percent error of l is simply: . Force is calculated by F=mg. Since g is a constant, we can just calculate the % error of the mass for the total % error of F. The formula for A is A=pr² à A=p(d/2)² à A=p(d²)/4. ‘p’ and ‘4’ are both constants and do not contribute error. Our measured length of ‘d’ is squared. This means we must multiply the percent error by 2 (power rule). . To calculate Dl, we must first find a: . We know that . By simple substitution, we can derive: . All operations are multiplication, division or tan/arc tan. Tangents do not alter error (there is no rule for tangents). We only have to add the percent errors of H, D and M_b. The percent errors for Dl and Young’s Modulus are as follows:

             Here is a comparison of GPE and accuracy % errors:

            As you can see, the actual % errors do not fall within the GPE % errors. This means that there are some errors contributed that do not come from the measurements. One area of error is when we approximated Dl by assuming a right triangle. Another error is caused by the bending of the wire by the mirror base as the collar moves downward (show in figure at right). Further more, error is also generated when the collar moves down and the mirror tips. The distance between the mirror and the board grows. We only measured from the board to the front groove on the platform. We never consider the minute distance between the groove and the mirror that grows gradually. Overall, the results of the lab were relatively accurate, especially considering the fact that the literature value might not be the right type of steel. Accuracy was within 16%. In the future, for more accurate results, we might try using another way of finding Dl that does not require estimation.

            Young’s Modulus is very similar to Hooke’s Law. We can put Young’s Modulus in the form of Hooke’s Law:

Hooke’s Law is F=kx. We can use the same variables in Young’s Modulus. Force (F) is the same in both equations. In Hooke’s Law, ‘x’ was the elongation of the object. In Young’s Modulus, the elongation is represented by Dl. In Hooke’s Law, ‘k’ was the spring constant, which depended upon the geometry and composition of the object. The Young’s Modulus only depends on the type of material (composition). Thus, ‘Y’ represents this. The last part of the equation, , the cross-sectional area over the length of the object, represents the geometry of the object. Each part of Young’s Modulus has been matched with the parts of Hooke’s Law. Thus, it can be concluded that Young’s Modulus is simply a more expanded form of Hooke’s Law. It divides the spring constant, ‘k’, into the object’s geometry and material. This way, there would be a unique Young’s Modulus for each type of material, while there could be numerous spring constants for different geometries of the same composition. However, these two formulas cannot be equated. The spring constant in Hooke’s law also depends on temperature, which Young’s Modulus does not incorporate. Therefore, Young’s Modulus must be calculated at a constant temperature.

            At the atomic level, the two concepts work similarly. Both measure the Force required for the expansion of the atoms of the object in relation to its composition and geometry. The composition of the object is important because, the denser the material, the tighter the bonds. Therefore, it would be harder to pull it apart. The types of bonds also affect the object’s elasticity. Both equations do not however consider the limit of elasticity for the object. If a graph were created with F and Dl as the axes, Dl would increase forever with F. This is unrealistic. The plasticity of the material would reach an end at some point, and the object would break.

Save or print this page

Back to Main Page